NEGATIVE NUMBERS – THE NUMBERS LESS THAN NOTHING

NEGATIVE NUMBERS – THE NUMBERS LESS THAN NOTHING

Introduction

The theme of eras of mathematics continues this week as for the last time we are going to learn the concept from the era before 500 BCE. This concept is all about something which is counted as nothing but consists of a value. A value that can be less than nothing. A value that doesn’t even have any value as such. Isn’t this confusing? The concept of negative numbers took a lot of time to come into existence as it was difficult for everyone to accept a concept less than zero.

Chinese rod system

The system which led to the invention of something less than zero by just thinking about the fact that if we get into a transaction where the buying price is greater than the cost price of the commodity, then the value counts to be a deficit and sums up to something which is less than zero. For example- if the price of the commodity is 100 and the commodity is sold at 90 then the deficit of 10 can be experienced as a negative value.

To cut short this issue, the Chinese rod system which had a symbolic representation of the numbers came into existence. The numbers in red were considered positive while the numbers in black were negative numbers. The numbers used here were to eliminate the red once and black once i.e., positive numbers and negative numbers whenever necessary in a particular transaction. The polarized nature of positive numbers (red rods) and negative numbers (black rods) also got tuned in with the Chinese concept that opposing but complementary forces—yin and yang—governed the Universe.

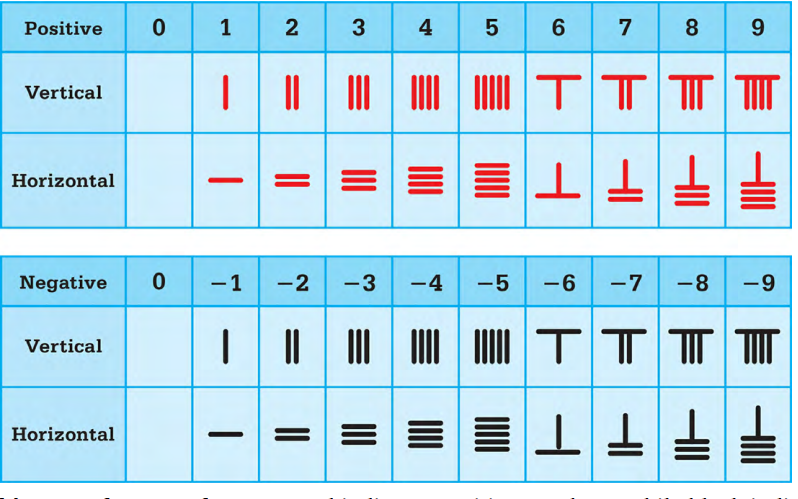
(Here the red rods indicate positive numbers and the black rods indicate negative numbers)

Fluctuating fortunes

Fortunes are the positive numbers used by the Brahmagupta and negative numbers were known as debts. Following conclusions were thus deduced :

This made no sense to the mathematicians working in the field of geometry as the figures and geometries have no negative factor.

Accepting the negative

The negative numbers were unacceptable for many years even after having many reasons for using and implementing it in life. One such example is using it for the temperature count. As this was representing the weather which goes from higher degrees meaning high temperature and lower degrees meaning low temperature. Zero degrees is the lowest temperature but then they also experienced lower degrees than zero so the negative numbers made it easy to justify the temperature.

Conclusion

The negative numbers are the numbers that came into existence after many questionable factors and unacceptance. But at last, this became the best important element in mathematics. The numbers used in many calculations, measuring temperature, etc. gave them the always-needed acceptance all over the world.